LETS Banking Systems Engineering Math
Banking System Blueprint
by John C. Turmel, B. Eng.
INTRODUCTION:
In GRACE AND MORTGAGE by Bishop Peter Selby, Bishop of Worcester,
ISBN 0-232-52170-0, page 116:
As Galbraith remarks, higher interest rates, it is hoped, "will
curb inflation." These comments of Galbraith illustrate why,
although
the raising of interest rates is the weapon against inflation chosen
by those who profit by it, it is also clear that as a method it cannot
finally work. John Turmel, a Canadian civil engineer and campaigner
against usury, has in two long articles brought algebra, plumbing and
poetry to bear on the task."
JCT: Just as ClimateGate exposed the big lie that CO2 is causing
global warming, InflationGate exposes the Big Lie of Economics
that interest fights inflation based upon the assumption that
inflation is more money chasing the same goods, Shift A, whereas
I've proven that it is actually the same money chasing less goods
after foreclosure, Shift B. Shift B inflation is unknown in economics
but the following analysis explains why inflation in Argentina went
from 1000% down to 36% after several provinces instituted local
provincial LETS bond currencies.
ANALYSIS:
The problem of exponential growth of debt is created within the
banking system and therefore a thorough understanding of the banking
system is helpful. The money system is the only mechanical system
which is under the jurisdiction of economists, not engineers.
Improvements are taking place in all system areas except the financial
system. It's time engineers turn their attention to this errant system
from which come all the financial woes of the world.
As an electrical engineer to have specialized in banking systems,
I will endeavor to explain the inner workings of this mysterious
system and its effects on users and debt. Though this might sound
daunting, I think I can present an easy way of handling subjects such
as:
- plumbing modeling of flows of money with pipes
- simple algebra
- exponential functions
- differential equations
- Taylor Series
- Laurent Series
- Laplace transformations
- control system circuitry
ECONOMIC FALLACIES
The two Big Double-thinks of Economics are that:
1) Banks lend their depositors' savings.
2) Interest rates fight inflation;
Banks do not lend out their depositors' funds, they lend out brand new
money. InflationGate means Interest does not fight inflation, it causes
it.
HOW BANKS CREATE MONEY
The inner workings of the engineering design of the global
"fractional reserve" banking system are mysterious to many
but no
matter how complex the actual process of creating money is, it can
accurately be simplified to "HAVING THE MONEY PLATES,"
whether they be
plates for changing metal to coins, plates for changing paper to
notes, or plates inside a bank's computer changing electrical blips to
bank deposits on which checks may be written.
Since changes in the money supply are regularly reported, money
must enter the supply from a source and leave through a sink. Our
liquidity system has both a tap and a drain. Since the government
borrows money itself, it does not have control of the tap. Who
controls the tap and the drain of the money supply?

The easiest way to model our system of financial liquidity is
with plumbing. All banking systems have the same exterior connections
to the economy.
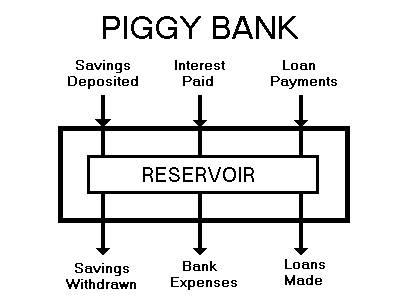
Fig. 2 is the interior plumbing of a piggy bank reservoir system
which shows that a deposit is first made into the reservoir and a loan
is then taken out of the reservoir which causes no increase in money
supply. Conversely, when a loan is paid, it goes into the reservoir
and there is no decrease in the money supply. A reservoir piggy bank
system does not affect the money supply because there is no tap and no
drain.
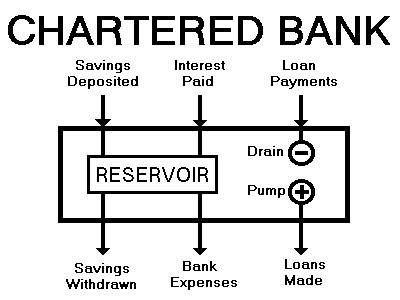
Though the Bank of Canada operates a tap and adds a small amount
of "high-powered" money to the money supply, Graham Towers, a
former
Governor of the Bank of Canada, pointed out that "The banks do not
lend out the money of their depositors. Each and every time a bank
makes a loan, new bank credit is created, new deposits, brand new
money." So a chartered bank has a tap and is not the pure
reservoir
system like a piggy bank model! Fig. 3 is the interior plumbing of a
chartered bank which shows that the loans do not come out of the
savings reservoir but come out of the tap of new money. When a
chartered bank makes a loan, the amount of money in circulation goes
up. When a loan is repaid, it goes down. In the textbook Economics
by Lipsey, Sparks, Steiner, it states "The banking system as a
whole
can create deposit money." Therefore, the banks all have their
very own
tap, their very own set of electronic money plates.
The famous "reserve ratio" of a "fractional reserve
system" sets
the limit on the amount of new money the private banks may create. It
simply means that a fraction of all deposits is sent to the Bank of
Canada's reservoir and the bank is then allowed to turn on the tap to
match the deposits remaining in their reservoir. Banks create most of
the money in circulation. To go step by step through the fractional
reserve banking system's plumbing with a 10% reserve ratio, let the
Bank of Canada turn on its tap and put $100 of "high-powered"
new
money into circulation. Each time a loan is made, the borrower always
eventually deposits it into the banking system.
| BoC | Saved Accts | IOU's | New$ | |
| Deposit old $100: | 10 | 90 | 0 | |
| Loan out new $90 for $90 IOU | 90 | 90 | ||
| Deposit new $90: $9 BoC $81 Bank | 9 | 81 | 0 | |
| Loan out new $81 for $81 IOU | 81 | 81 | ||
| Deposit new $81: $8 BoC $73 Bank | 8 | 73 | 0 | |
| Loan out new $73 for $73 IOU | 73 | 73 | ||
| [...............................] | ||||
| Deposit new $10: $1.00 BoC $9.00 Bank | 1 | 9 | 0 | |
| Loan out new $9.00 for $9.00 IOU | 9 | 9 | ||
| [............................... to infinity] | ||||
| -------- | ------ | ------- | ------ | |
| $100 | $900 | $900 | $900 | |
| Old | New Savings | New | New$ |
Where the system started with only $100, after the expansion is
over, the Bank of Canada is holding the original $100 as the banks'
10% reserves and the banks' reservoirs are holding the other $900 of
the savers' new deposits. So, $900 newly created dollars were added to
the system by the private fractional reserve banks for every $100
issued by the Bank of Canada. This limit is the inverse of the reserve
ratio. A reserve ratio of 5% would generate total new money of 1/.05 =
20 times the initial high-powered Bank of Canada money. This is how an
ordinary bank creates new money as new loans based not on the
production possible but on past savings of money.
Monetary reformers who think that money issued by the banks is
fraudulent valueless money are incorrect. It is evident that all the
new money issued is originally backed up by collateral or personal
IOUs pledged at the time of the loan.
Monetary reformers who think that banks use $100 to lend out $900
and collect interest on the whole $900 are incorrect. It is evident
that most interest is paid to depositors and used for expenses at
every stage. I call this belief the "Voorhis Mistake." Sorry
Jerry. You
were right on so much else. .
HOW BANKS DESTROY MONEY:
Just as money is newly issued from the tap when a bank makes a
loan, money is destroyed down the drain when a borrower makes a
principal payment. Interest payments go back into the reservoir and
not down the drain.
When a large withdrawal is made or a large failure is written off
the banks' books, the reverse reserve ratio process takes place. Since
losses are covered from reserves upon which are based the loans, when
their reserves go down, they have to call that amount in loans. It's
quite an automatic doomsday mechanism. It was bankers calling in loans
which precipitated the 1929 stock market crash. As people fail to meet
their call and those loans are written off again reducing the bank
reserves, more loans must again be automatically called in. The
process gets worse and causes the banking system to fail.
Any cabal of rich men can precipitate such a "credit
crunch" by
simply moving their savings to another country which forces the banks
in the target country to start calling in loans. Such private power
over the world's financial system is inappropriate.
HOW BANKS CONCEAL THEIR CREATION OF MONEY:
The injection of new money from their taps has been well hidden
from the public view because the Bank Act insists that before any new
money may be loaned into circulation, old money must be deposited into
their reservoirs. It's just as if a casino were to insist on old chips
being put into the safety deposit section before it would issue new
chips. By merely matching new loans to deposits, this brilliant cover
for the turning on of the tap misleads observers into falsely
concluding that a chartered bank operates like a piggy bank. With a
lawful reason to seek deposits before they can lend, there is no
outward difference between chartered bank and a piggy bank. Yet, banks
do not seek deposits to lend to other people. They seek them to
lawfully turn on the tap of new money leaving depositors' old deposits
in their accounts.
It's a fascinatingly tricky mechanism but it's purpose is to
foster the impression that borrowers are getting savers' deposits and
that savers therefore deserve to get interest for lending borrowers
their money. This may have surely been true when banking did operate
like a piggy bank without the creation of new money but it certainly
is not true now that banks operate more like a casino banks issuing
new liquidity. The matching of loans to deposits successfully hides
the fact that no one is giving up the current use of their money since
it is new money being loaned out and therefore no one is being
deprived of the use of their money.
DOUBLE-THINK #1
Understanding now where bank loans come from, we can see the
double-think that has been brainwashed into economic thinking.
According to George Orwell in "1984," to double-think was
having the
ability to accept two contradictory points of view as both
simultaneously true.
I noted a perfect example of economic "double-think" in an
article on the sci.econ Usenet newsgroup on Aug 24 1995 by
wfhummel@netcom.com (William F. Hummel). In one paragraph, he said:
"A
bank loans money that it receives from other depositors..." This
is
exactly how everyone thinks a savings bank works, just like a piggy
bank. No source of new money, no tap. Just a reservoir.
In another paragraph, he said: "The money supply increases
whenever a bank creates a new loan, and it decreases when the loanee
pays off the loan."
Both these statements cannot be true. Either borrowers are
getting savers' deposits or they are getting new deposits. Though we
know this is true that piggy banks lend out their depositors' savings,
we also know that it is not true of the private chartered banks which
are lending out new money which is expanding the money supply. This is
one of the great double-thinks of economics. The more you've studied
economics, the more you learn to believe that loans going out are new
money at the same time as being old money.
Try it. Ask any economist where the banks get the money from
their loans, 99% will answer "from their depositors." Then
ask if it
isn't true that economics books say that banks are creating new money
when they make loans and they'll agree right away without realizing it
has just contradicted their previous belief that these new loan funds
were depositors' old savings funds.
REAL POWER OF CONTROL OF LOAN CREATION:
The real power of banking is being able to refuse to turn on the
loans tap for one businessman and foreclose while turning it on for a
new loan to another businessman so he can buy out the first
businessman at auction.
CASINO BANK
The major difference between a casino bank and a chartered bank
is that the liquidity from a casino bank never suffers inflation while
the liquidity from a chartered bank always suffers inflation. Since
the hardware of a casino bank, chips of different colors and
denominations, is functionally identical to the hardware of a
chartered bank, computer credit pulses and coins or paper of different
colors and denominations, inflation is not a hardware problem. It is a
software problem. There is something wrong with the software program
which regulates how money is put into and taken out of circulation.
There is nothing wrong with the hardware. It is the operators of the
taps who are improperly restricting the flows.
To fully appreciate our present predicament, consider a station-
master in a wartime situation who was ordered to ensure that an
invading army did not capture the rail system in operating condition
and burned all of the railroad tickets. Our failure to use our
manpower, materials and tools because there are insufficient monetary
tickets puts us in the same category as the invading army who failed
to use the captured railway because they couldn't find any railway
tickets. To get out of this silly predicament, public control of the
money tap must be regained from the private banks.
HOW "MORT-GAGE" INTEREST CREATES A DEATH-GAMBLE
csurvive the mort-gage death-gamble.
P < principle, I < Interest, i < Interest Rate, t < Time
| Production Costs (Principal) | 100 | P | 1 | |
| Production Prices (Debt) | 100+I | P+I | exp(it) | |
| Purchasable Value (Survivors) | 100/(100+I) | P/(P+I) | 1/exp(it) | |
| Unpurchasable Value (Non-survivors) | I/(100+I) | I/(P+I) | 1-1/exp(it) | |
| For Unemployment = 0, let: | I=0 | I=0 | i=0, t=0 |
The odds of survival are always set by the interest rate(i).
P/(P+I) survive, I/(P+I) do not.
There is a tricky way to avoid the death-gamble in a mort-gage contract!
If it's a problem borrowing 10 and owing 11 at the end of the contract,
the simplest solution is to pay the interest up front so you can earn the 10th
chip from the banker before you have to pay off the 10! If you paid Principal
up front, that would go down the drain and you can't earn it back. But paying
the interest up front goes into the reservoir of existing money. By paying the
interest up front rather than at end converts the unpayable usury into a
payable service charge! If only the suckers knew.
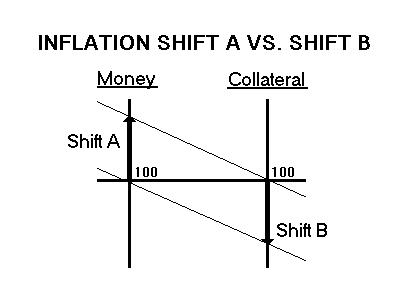
INFLATION
The equation for the minimum inflation (J) we must suffer is the
same as the equation for unemployment (U) because the fraction of the
people foreclosed on is the fraction of collateral confiscated. Though
we
are led to believe that inflation is caused by an increase in the money
chasing the goods (Shift A), actually, it is caused by a decrease in
the
collateral backing up the money (Shift B) due to foreclosures. Though
both inflations shifts feel the same, the graph shows inflation is not
the
inverse function of interest, it is the direct function exposing the
Big Lie
that interest fights inflation. (Fig. 4)
Most people who have not studied economics, if asked whether
interest fights or causes inflation, are quick to agree that a
merchant must pass on increased interest costs in his prices and
therefore it is evident that increased interest costs will result in
increased prices. How they then accept politicians who tell them
interest fights inflation is a measure of double-think too.
DIFFERENTIAL EQUATIONS
Where "B" is the original bank balance, "i" is
the rate of
interest and "t" is time, the differential equation for your
bank
account is:
dB/dt = iB
The "d" stands for "delta" or
"change."
So "dB" is the delta change in the Balance.
So "dt" is the delta change in the time.
So the rate of change of your bank balance over time equals your
balance times the interest rate: iB. We can now examine the problem,
not over one cycle with algebra, but over time with exponential
functions. The solution to the differential equation dB/dt=ib is
exp(it). Exp(it) means that your balance will exponentially double and
double in time as a function of the interest rate. It is a crooked
non-linear function.
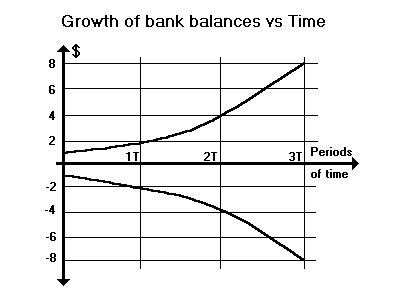
Consider that if two men are in a car accident and one owes the
other $1. Fig. 5 shows that if there is no interest, the debt stays
friendly and sociable like the two straight lines for one owing $1 and
the other being owed $1. The two straight lines from at +$1 and -$1
represent the growth of their debt and credit. Zero growth. If there
is interest, the balances start to grow with time and double in time
T, then again in time T and again and again into the exponential curve
exp(it).
LAPLACE TRANSFORMATIONS
Laplace Transformations are a branch of mathematics which allows
engineers to manipulate complex system differential equations
algebraically. Like magic, we transform tough real world functions
from real numbers into a function of the Laplace variable "s"
in the
imaginary number dimension. There we do our computations algebraically
and then reverse transform from the imaginary number dimension to the
real world solution. Nothing in my engineering studies has ever awed
me as being more powerful than Laplace Transforms and what can be done
with them.
TAYLOR SERIES
We want to get the Laplace transform of a bank account which
makes an original Balance B grow as B*exp(it). We expand the bank
account function exp(it) into it's Taylor Series:
exp(it) = 1 + it + (1/2!)*(it)^2 + (1/3!)*(it)^3 + ...
LAURENT SERIES
Taking the Laplace Transform of each component of the Taylor
Series produces the Laurent Series of the banking system:
LT{exp(it)} = LT{1 + it + (1/2!)*(it)^2 + (1/3!)*(it)^3 + ...}
LAURENT SERIES = 1/s + i/(s^2) + i^2/(s^3) + i^3/(s^4) + ...
= (1/s)*(1 + i/s + (i^2)/(s^2) + (i^3)/(s^3) + ...)
= (1/s)*(1/(1-i/s))
= 1/(s-i) = USURY BANK ACCOUNT LAPLACE TRANSFORM
The moment the debt passes through the (1/(s-i)) usury filter in
banking system, it starts to grow.
The differential equation for inflation (J) whose solution is (1-
exp(-it)) can be described as:
dJ^2/dt^2 + (i)*dJ/dt = 0 or j'' + (i)j' = 0
The Laplace Transformation of the inflation (J) is: 1 / ( s^2 + is )
CONTROL SYSTEMS
With the Laplace transform, it is also possible to draw the
electrical blueprint of a bank account in the usury banking system:
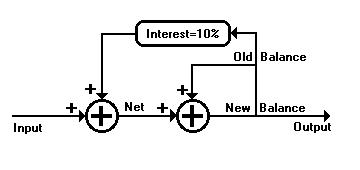
Fig. 6 is the control system blueprint of a usury bank account
which shows that added to any input is the feedback of the interest
rate times the previous balance which can be positive or negative.
This net amount is added to the previous balance to produce the new
balance. This positive feedback makes the system unstable and the root
of bad vibrations.
Your $100 volt pulse is the input to the first addition node.
Added to it is the positive feedback interest voltage from the last
balance which, to start, was 10% of zero volts. The new net $100 volt
pulse enters the second addition node where it also is added to the
old balance, still zero volts, to push the new balance up to $100
volts.
Next year, with no new pulse at the input, added to this zero
voltage is 10% interest, a pulse of 10 volts. The 10 volt pulse goes
into the second addition node where it is added to the old balance,
100, to push the new balance to 110.
After 2 years, you'll have 11 more for a balance of 121.
After 3 years, you'll have 12 more for a balance of 133.
After 4 years, you'll have 13 more for a balance of 146.
After 5 years, you'll have 14 more for a balance of 160.
After 6 years, you'll have 16 more for a balance of 176.
After 7 years, you'll have 18 more for a balance of 194.
After 7.2 years, you'll have 6 more for a balance of 200.
The same growth will apply to an input of -100 volts.
This demonstrates quite well what's called the "rule of
72."
Divide the number "72" by the percent interest, in this case
10%,
and that's approximately the number of years it will take to double,
in this case 7.2 years, and double, and double, etc. That's what's
called an exponential function.
At 5%, it should take about 14.4 years to double.
At 10%, it should take about 7.2 years to double, as shown.
At 24%, it should take about 3 years to double.
Cycle after cycle with no new inputs, you have the exponential
growth exp(it) which grows as the above series. It acts just like
bringing a microphone up to a speaker. The sound from the speaker is
picked up by the microphone and fed back to make the sound out of the
speaker louder which is picked up and fed back to make it louder until
you blow your speaker. Having an unstable positive feedback loop built
into a system makes that system unstable.
Negative feedback loops where the feedback from the previous
balance is subtracted are very useful in stabilizing systems away from
error but positive feedback always makes the error grow. A physical
example of negative, positive and no feedback follows:
If you have a bowl and you put a ball in it and then give the
ball a little shove, it will travel up one side, gravity will bring it
down and it will rock back and forth until it settles back to the
middle. That's how engineers use negative feedback to bring back
things which have been pushed out of normal operation back to normal.
If you turn the bowl upside down and put the ball at the top, one
small push and the gravity will make the ball fall faster and faster.
That's unstable. If you put the ball on a platform and give it a push,
without friction, it will just continue in rolling steady state. Both
zero and negative feedback are acceptable while positive feedback is
always unacceptably unstable.
Engineers say that systems are stable if the pole of the system
is in the left-hand plane or on the origin but unstable if the pole is
in the right-hand plane.
Knowing that the Laplace Transform of the system is 1/(s-i), the
denominator is zero when s=+i and therefore, the pole is on the right-
hand side of the origin, hence unstable.
Eliminating the bad vibrations is as simple as making the
interest feedback loop in the bank's computer programs zero and using
only the simple interior circuit known as an "integrator."
Currency
systems presently using these simple "integrator" accounts
are now
known internationally as Greendollar systems of the Local Employment
Trading System (LETS).
We know that the LETSystem is an interest-free system and so we
cut the positive feedback loop to get 1/(s-0). Fig. 7 shows that to
make the interest positive feedback zero, we simply break the circuit:
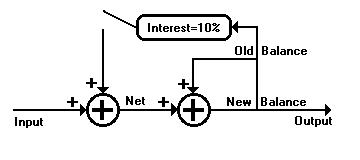
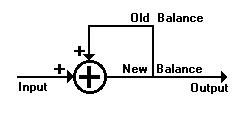
Fig. 8 is the interior circuit still left in operation which is the
true
electrical control system of the LETS 1/s bank account. This
is the mathematical circuitry behind all interest-free systems and how
Greendollars work: Instead of an output which is exponential, crooked,
we have an output which is linear, straight. Your $100 volt pulse is
the
input to the addition node. Added to it is old balance, starting at
zero, to
push the new balance up to $100 volts.
Next year, with no new pulse at the input, and with interest
voltage to add, the balance stays at $100 volts. If another deposit
comes in, it's added to the old balance to create a new balance. A
negative coming in will reduce the old balance. But the system is
always in balance. Positives equal negatives.
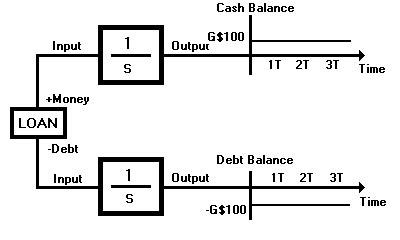
So now we see how Greendollar credit at a LETS bank works. Fig. 9
shows that when you use Greendollar credit, the amount you have taken
out which is represented by the top circuit and the amount you owe
which is represented by the bottom circuit stay the same:
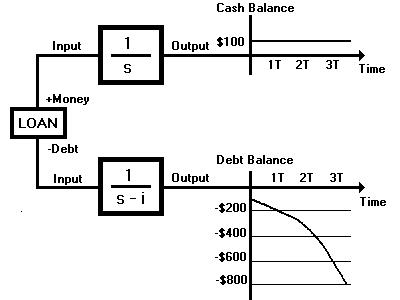
We can also see how a loan at a normal usury bank works. Fig. 10
shows that while the amount of cash in your wallet is shown by the
upper circuit, the debt for that $100 shown in the lower circuit
starts to double and double over time and all the while, all you have
is original $100 in your possession:
This analysis shows that unemployment and inflation must go to
zero if the banks' computers, which are now permitted to charge both
interest and service charges, are restricted to only the service
charge and the interest charge abolished.
Note that the exponential derivation shows that there are two
solutions to the mort-gage (death-gamble). The software solution is
interest rate(i) = 0 by restricting the banks computers to a pure
service charge and abolishing the interest charge. The hardware
solution is time(t) = 0 by installing an instantaneous electronic
cashless marketplace.
GAME MODEL: SERVICE CHARGE VS. INTEREST
In his book `The Theory of Games and Economic Behavior', John Von
Neumann, one of this century's top mathematicians, stated that
"important questions in economics arise in a more elementary
fashion
in the theory of games." In the business war for markets, the
economy
decides who sells their goods and who fails to. Models used by
economists are flawed by guesses and approximations about what the
economy will choose. The only way to perfectly model the economy is to
use fair chance to pick the winners and losers.
TO PLAY MORT-GAGE:
The necessary game equipment to play "mort-gage" is:
1) 3 types of tokens to represent food, shelter, and energy (the
tokens can be knives, forks, spoons)
2) a fair chance mechanism like a coin, cards, dice, etc.;
3) matches, beans, chips or tokens to represent currency.
Here is how I demonstrated the difference at a dinner party
between the interest on a business loan and the service charge on a
Greendollar LETSystem business. The hostess provided a bag of raw
beans which I used as my model dollars. I used knives as tokens for
food, forks as tokens for clothing and spoons as tokens for services
which I put into a bowl representing the market economy in the center
of the table.
INTEREST-USURY MARKETING METHOD:
In the Interest Game, all borrow 10 but have to inflate their
prices to recuperate the 11 they owe the bank.
Step 1): I had all 10 guests at the table pledge their watch as
collateral for a $10 Beandollar loan. At 10% interest, they each owed
me 11 Beandollars at the end of the loan period.
Step 2) I had all 10 guests spend their $10 Beandollars into the
market bowl in exchange for a product token.
Step 3): Once all 10 guests now had a product token for sale, I
used fair chance to determine who would successfully market their
product. Starting first with pairs of players with similar product
tokens for sale, I flipped a coin to determine which the economy chose
to buy from. Then winner delivered the product token to the market
bowl and collected $11 Beandollars. After the first round, half the
players had successfully marketed their product and half had not yet
sold. Finally, taking diverse pairs, I continued tossing the coin to
decide who the economy chose to purchase from, the winner delivering
goods and taking price out of the market.
Step 4) Since everyone put in 10 and the winners all took out 11,
eventually, the market bowl ran out of Beandollars with one guest
still having products unsold. I foreclosed and seized the loser's
product token and watch.
Step 5) I explained to the winners how their $100 Beandollars had
inflated because there were now only 9 watches.
NO-INTEREST LETS MARKETING METHOD:
In the No-interest Service Charge Game, all guests borrowed 11
and owed 11. The 11th Beandollar borrowed was to pay the bank
employees a service charge.
Step 1): I had all 10 guests at the table pledge their watch as
collateral for an $11 Beandollar loan.
Step 2) I had all 10 guests spend the same $10 Beandollars to
purchase their production token from the market bowl and then spend
their last Beandollar into the market to pay for the services of the
bank employees who facilitated the transactions.
Step 3): I again used the coin to model the decisions of the fair
market and noted that at the end of the game, all the production was
sold.
Step 4): I noted that no one lost their watch even though the
bankers still got paid.
Step 5): I noted that at the end of the LETS service charge game,
there were enough watches for the Beandollars to retain their original
value, unlike in the Interest Game. I noted that everybody had sold
all their product tokens because the 11th unit of money had entered
the market bowl through the bank employees' service charges.
The very subtle difference between systems is that in the
Interest Game, the bank demands payment of money it did not create
while in the LETS Service Charge Game, the bank demands payment of
money it did create. With exactly enough markets to match the prices
of goods produced, there can be no foreclosures.
EQUATION OF RESPONSIBILITY:
This is the argument I offered the Supreme Court of Canada in
1982 about the UNICEF 1981 estimate of starving children: 46,000/day.
Unfortunately, only the software solution can be implemented now.
Being generous in assuming that the rate of children perishing due to
starvation on the planet will remain constant given the recent flurry
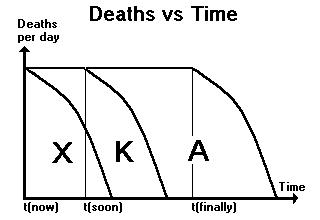
of foreclosures on farm production, Fig. 11 shows the death curve.
Since this software change in the computer's programming is quite
instantaneous, if it were to be ordered at time t(now) and the bank`s
computers immediately restricted to a pure service charge, all those
industries that have recently died will be resurrected by an infusion
of interest-free credit that will allow them to start rehiring as fast
as they start writing new paychecks that need only be exchanged for
work as collateral. This will generate the greatest industrial boom
imaginable. The increase in production would cause the slope of the
death curve to change downwards until the eventual eradication of
starvation due to the maximization of our industrial capacity. Area X
under the death curve represents the number who will perish even if we
flip the economic engine to full power at time t(now) because we won't
be able to get to them in time.
Delaying the switch to full power till time t(soon) delays the fall of
the curve causing the area under it to increase by a statistically
measurable amount K. Fortunately, the curve must come down at time
t(finally) when the hardware solution is finally implemented by
cashless money transfers.
The hardware solution nullifies the gage (gamble) portion of the
mortgage death-gamble in making the communications so good as to
guarantee sure gambles! Today entrepreneurs gamble on their wares
being sold and the weakest are put out of production. Inflation
through confiscation now occurs. This cannot occur in the electronic
medium available in our near future.
When communications become that fast, the slope of the death curve
will change downward until the certain elimination of starvation,
since food production will become a sure thing. The total area under
the curve represents the maximum number of souls who will perish even
if the software solution is never implemented. Though the curve must
eventually come down by the electronic revolution, hastening the
change of slope to time t(now) causes the area under the curve to
decrease saving a statistically measurable slab of humanity A. For
anyone with the power to hasten or delay the software solution,
realize upon reading this that this is your Judgment Day in that there
is now a slab out there with your name on it that is growing and
whether it is a death(K) or a life(A) slab depends purely on your
decision right now.
DEATH RATE VS TIME PARALLELOGRAM
It can easily be shown by the parallelogram theorem that the area in
the K slab of the Keepers of the Interest Act is equal to the area
covered during the delay. So, the K slab representing the number of
souls to be lost due to the extra delay is equal to the number of
souls who perish during the delay.
Using the UNICEF estimate of the number of children who perished in
the global village in 1981, 17,000,000, we can now accurately scale
the death curve to get a good idea of the stakes we are gambling. The
daily death rate of children in 1981 was therefore 46,000 per day.
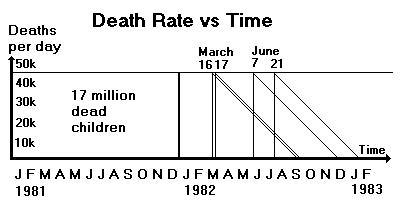
The area between the date of the Court of Appeal hearing on March
16,
1982, and the date of this hearing on June 21, 1982, represents the
number of children who will perish as a direct result of the Court's
failure to comprehend the seriousness of the matter. The number who
will perish as a result of their 97 day delay is equal to the number
who perished during the delay. 46,000 dead children per day times 97
days equals 4,462,000 children who will not live who should have.
Nothing can be done to undo that fact though the magnitude of their
error can be held to a minimum by the immediate solution.
It was to stress the importance of hastening the software solution by
even one day that I sought an Order of Mandamus that the Crown enforce
the Criminal Code Sections against Gerald Bouey one day before this
appeal was to be heard on the morrow in full court.
On Mar 15, Justice Blair had wanted to put off his decision until the
ruling on the morrow of the court in the Mar 16 hearing but the Crown
objected. I explained that given the money system is now 90%
electronic and vulnerable at its central computer to instantaneous
correction, I likened our problem to that of the astronaut attempting
to pull the plug on the killer computer in the movie "2001 A SPACE
ODYSSEY." I stated "Here we sit in front of the killer
computer's
plug. I'm a scientist and I say pull the plug and our mortgage death-
gamble will be over."
It is simple to prove that since the Canadian banking system is
international, if and when it changes to a pure service charge, the
usury banking system will collapse globally. It was to try and save
one day's worth of children, 46,000 souls, that I asked for the
electronic solution one day earlier. Justice Blair decided that he
would not extend time on the matter and dismissed the motion without
costs.
Nevertheless, anyone standing in the way of the quickest
implementation of Global LETS has a K-slab growing from the moment
they realize that LETS funding is the solution to the extinction going
on around us.
I hope this analysis has helped clear up many of the formerly
misrepresented and misunderstood aspects of the usury banking
system as well as explain why usury has been condemned
throughout
history as the greatest crime against humanity. InflationGate is
the only
thing standing between mankind and abundant salvation.